Aviso: Este post foi traduzido para o português usando um modelo de tradução automática. Por favor, me avise se encontrar algum erro.
Agora que vimos o que são os embeddings, sabemos que podemos medir a similaridade entre duas palavras medindo a similaridade entre seus embeddings. No post de embeddings vimos o exemplo do uso da medida de similaridade por cosseno, mas existem outras medidas de similaridade que podemos usar, como o quadrado L2, a similaridade do produto escalar, a similaridade por cosseno, etc.
Neste post, vamos ver essas três que mencionamos.
Similaridade pelo quadrado L2
Esta similaridade é derivada da distância euclidiana, que é a distância em linha reta entre dois pontos em um espaço multidimensional, que é calculada com o teorema de Pitágoras.
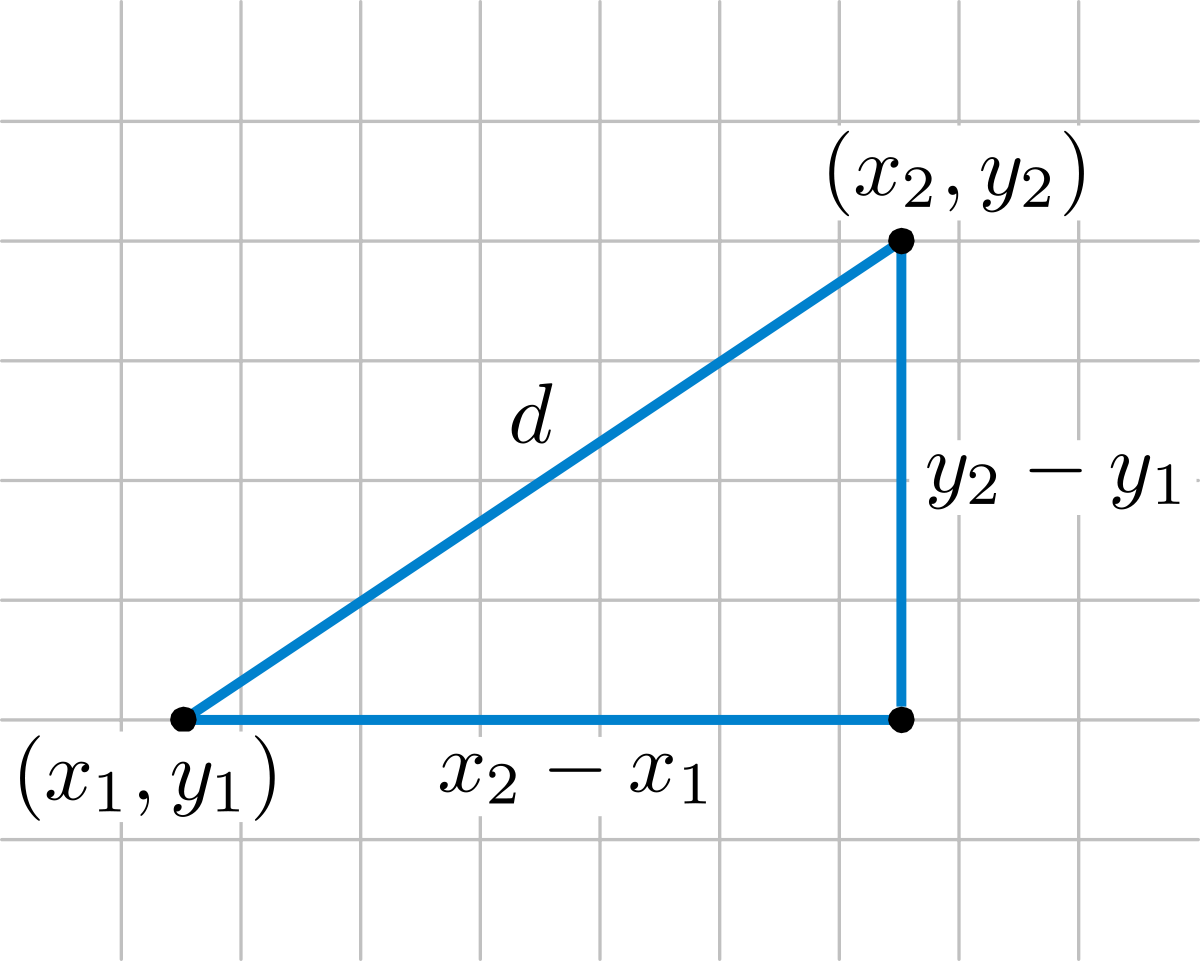
A distância euclidiana entre dois pontos p e q é calculada como:
d(p,q) = √((p1 - q1)2 + (p2 - q2)2 + ··· + (pn - qn)2) = √(∑i=1n (pi - qi)2)
A similaridade pelo quadrado L2 é o quadrado da distância euclidiana, ou seja:
similidade(p,q) = d(p,q)2 = ∑i=1n (pi - qi)2
Similaridade cosseno
Se lembrarmos do que aprendemos sobre senos e cossenos na escola, lembraremos que quando dois vetores têm um ângulo de 0º entre eles, seu cosseno é 1, quando o ângulo entre eles é de 90º, seu cosseno é 0 e quando o ângulo é de 180º, seu cosseno é -1.
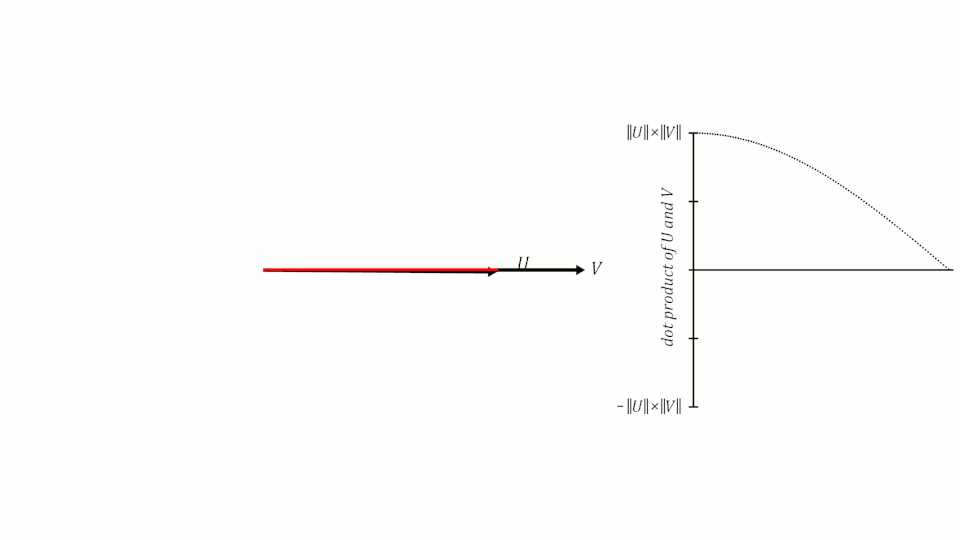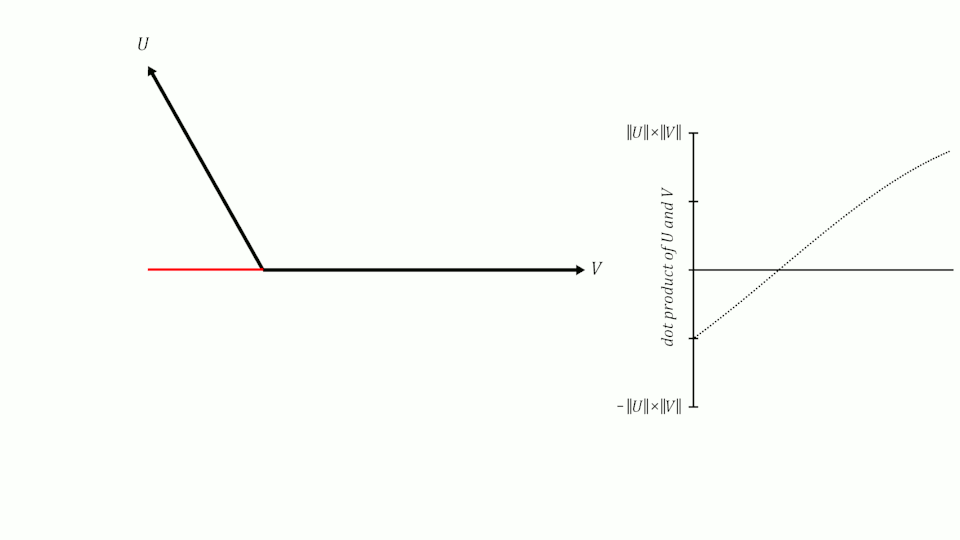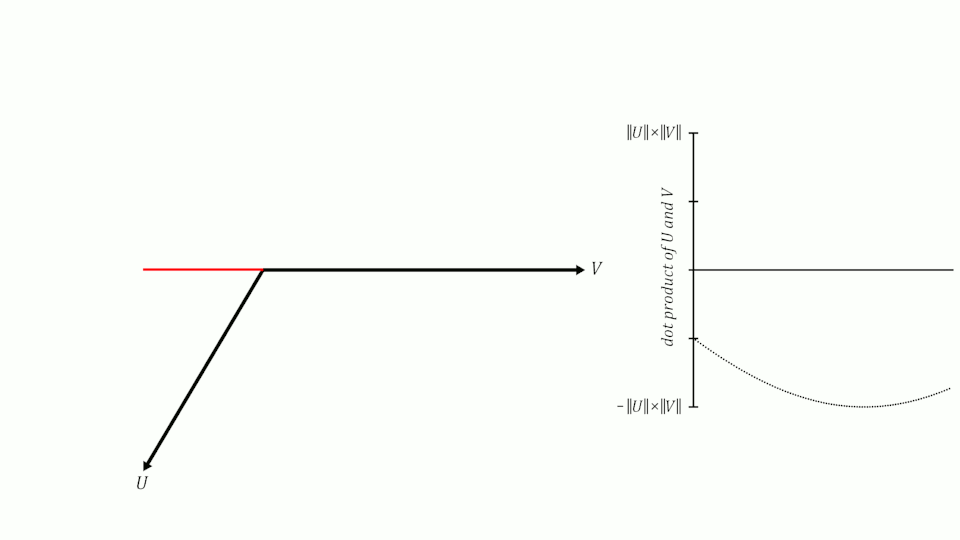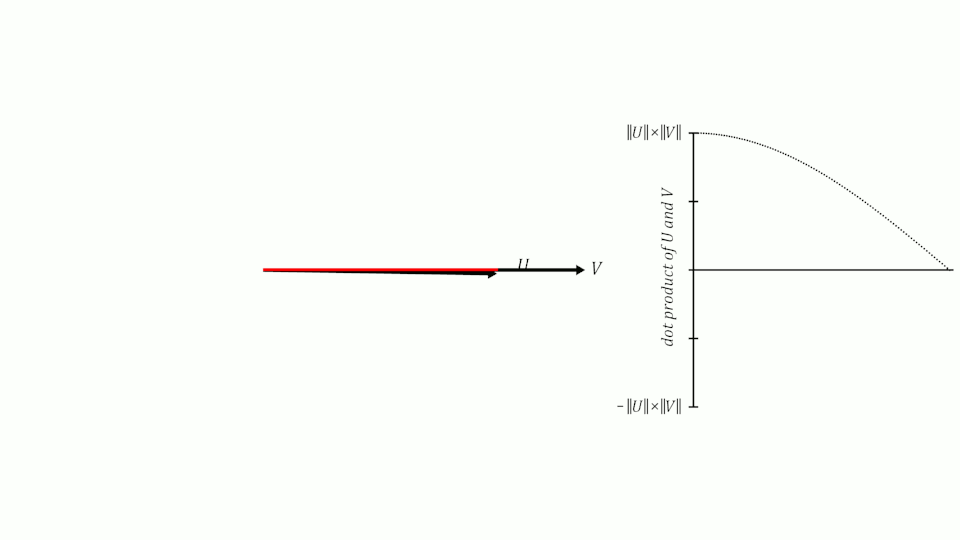
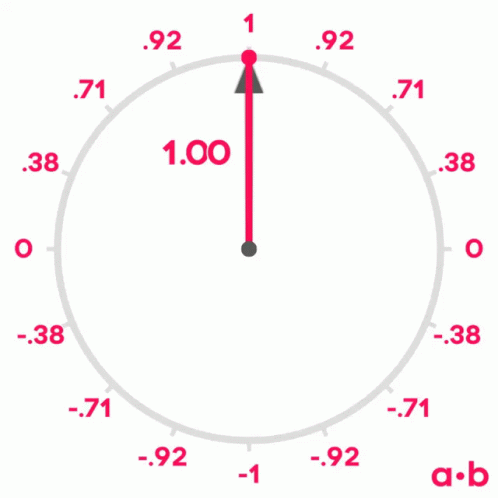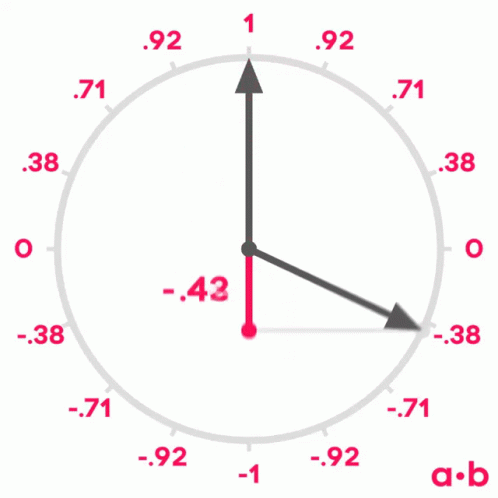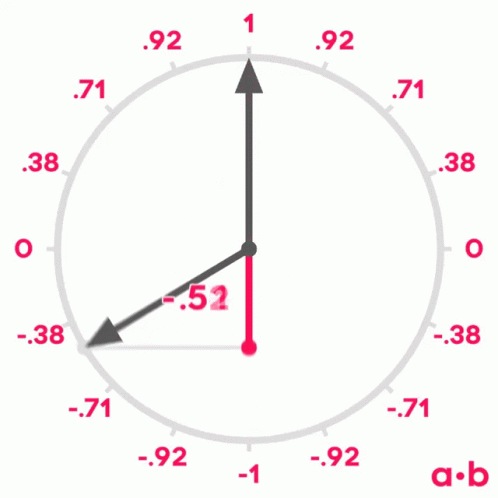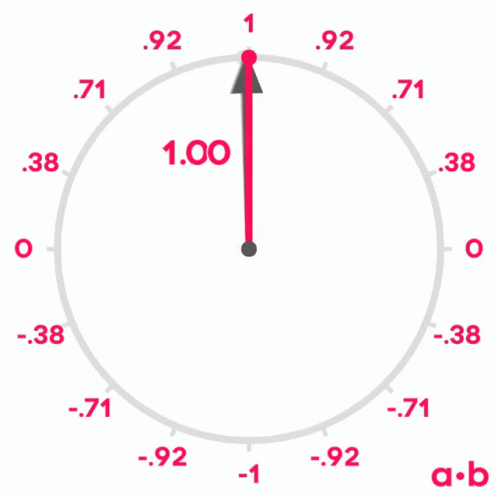
Portanto, podemos usar o cosseno do ângulo entre dois vetores para medir sua similaridade. Pode-se demonstrar que o cosseno do ângulo entre dois vetores é igual ao produto escalar dos dois vetores dividido pelo produto de seus módulos. Não é o objetivo deste post demonstrá-lo, mas se quiserem podem ver a demonstração aqui.
similitude(U,V) = U · V||U|| ||V||
Similaridade do produto escalar
A similaridade do produto escalar é o produto escalar de dois vetores
similaridade(U,V) = U · V
Como escrevemos a fórmula da similaridade cosseno, quando o comprimento dos vetores é 1, ou seja, estão normalizados, a similaridade cosseno é igual à similaridade do produto escalar.
Então, para que serve a similaridade pelo produto escalar? Para medir a similaridade entre dois vetores que não estão normalizados, ou seja, que não têm comprimento 1.
Por exemplo, o YouTube, para criar os embeddings dos seus vídeos, faz com que os embeddings dos vídeos que classifica como de maior qualidade sejam mais longos do que os dos vídeos que classifica como de menor qualidade.
Desta forma, quando um usuário faz uma pesquisa, a similaridade pelo produto escalar dará maior similaridade aos vídeos de maior qualidade, portanto fornecerá ao usuário os vídeos de maior qualidade em primeiro lugar.
Qual sistema de similaridade usar
Para escolher o sistema de similaridade que vamos usar, devemos ter em conta o espaço no qual estamos trabalhando.
- Se estivermos trabalhando em um espaço de alta dimensionalidade, com embeddings normalizados, a similaridade cosseno é a que melhor funciona. Por exemplo, a OpenAI gera embeddings normalizados, portanto a similaridade cosseno é a que melhor funciona.
- Se estivermos trabalhando em um sistema de classificação, onde a distância entre duas classes é importante, a similaridade pelo quadrado L2 é a que melhor funciona.
- Se estivermos trabalhando em um sistema de recomendação, onde a comprimento dos vetores é importante, a similaridade do produto escalar é a que melhor funciona.