Como funcionam as Redes Neurais: Regressão Linear e Descida do Gradiente passo a passo

04 de outubro de 2025

Aviso: Este post foi traduzido para o português usando um modelo de tradução automática. Por favor, me avise se encontrar algum erro.

Como dissemos, um neurônio é uma unidade de processamento, recebe alguns sinais, realiza alguns cálculos e produz outro sinal.

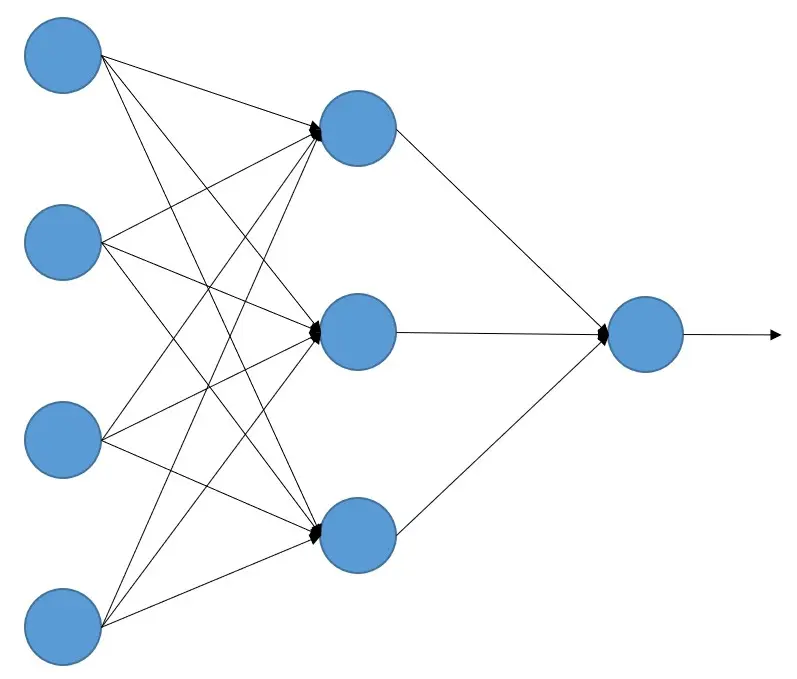
Então vamos ver o exemplo mais simples, o caso em que se recebe um sinal e se obtém outro, e vamos ver isso com a regressão linear.

!red neuronal regresión

Suponhamos que fizemos algumas medições e obtemos os seguintes pontos

	
		import numpy as np
 
x = np.array( [ 0. , 0.34482759, 0.68965517, 1.03448276, 1.37931034,
        1.72413793, 2.06896552, 2.4137931 , 2.75862069, 3.10344828,
        3.44827586, 3.79310345, 4.13793103, 4.48275862, 4.82758621,
        5.17241379, 5.51724138, 5.86206897, 6.20689655, 6.55172414,
        6.89655172, 7.24137931, 7.5862069 , 7.93103448, 8.27586207,
        8.62068966, 8.96551724, 9.31034483, 9.65517241, 10. ])
 
z = np.array( [-0.16281253, 1.88707606, 0.39649312, 0.03857752, 4.0148778 ,
        0.58866234, 3.35711859, 1.94314906, 6.96106424, 5.89792585,
        8.47226615, 3.67698542, 12.05958678, 9.85234481, 9.82181679,
        6.07652248, 14.17536744, 12.67825433, 12.97499286, 11.76098542,
       12.7843083 , 16.42241036, 13.67913705, 15.55066478, 17.45979602,
       16.41982806, 17.01977617, 20.28151197, 19.38148414, 19.41029831])
	
	
		
	
	Copied

	
		import matplotlib.pyplot as plt
 
plt.scatter(x, z)
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como vemos, isso pode se assemelhar a uma regressão linear. Ou seja, podemos supor que o neurônio recebe x, multiplica por um número e gera z.

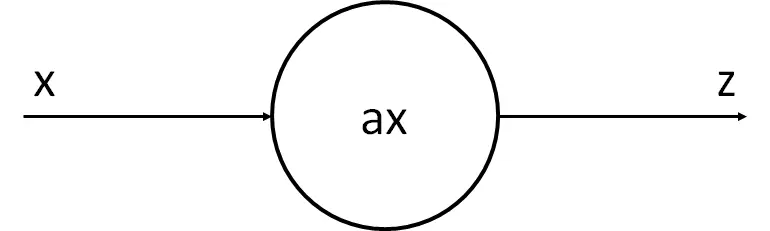
A partir daqui vamos mostrar como funcionam as redes neurais, só que com um exemplo simples de um único neurônio, depois vamos apresentar exemplos cada vez mais complexos, até explicarmos o funcionamento geral das redes neurais. Mas se você entender o que vai acontecer a seguir, vai entender as redes neurais.

Nossa neurônio tem o parâmetro a, que é o que queremos modificar para que a reta que vai gerar se assemelhe o máximo possível aos pontos. O processo de aprendizagem do nosso neurônio vai consistir em, por meio de alguns cálculos, determinar o melhor valor possível de a

Inicialização aleatória do parâmetro

Este exemplo é simples, mas quando temos redes neurais complexas e não sabemos quais valores seus parâmetros devem ter, o que se faz é inicializá-los aleatoriamente

	
		import random
 
random.seed(45) # Esto es una semilla, cuando se generan números aleatorios, 
                # pero queremos que siempre se genere el mismo se suele fijar
                # un número llamado semilla. Esto hace que siempre a sea el mismo
 
a = random.random()
a
	
	
		
	
	Copied

	
		0.2718754143840908

O valor de a é 0.271875, vejamos que reta obteríamos se parássemos agora

	
		z_p = a*x
 
plt.scatter(x, z)
plt.plot(x, z_p, 'k')
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como vemos, não se parece em nada, então vamos ter que fazer com que nosso neurônio *aprenda*

Cálculo do erro ou loss

Para buscar o melhor valor possível de a, queremos encontrar um valor que faça com que os valores previstos pela nossa neurônio tenham o menor erro possível em relação aos valores reais de z.

Neste tipo de problemas costuma-se utilizar o erro quadrático médio (EQM) ou mean squared error (MSE) em inglês. Existem muitas outras funções de erro, mas por enquanto isso não vem ao caso, então fique com essa e aprenderemos mais funções adiante.

Na literatura, esse erro geralmente é chamado de função de perda ou loss function, portanto, a partir de agora iremos chamá-lo assim.

O erro quadrático médio (EQM) mede a distância entre os pontos previstos por nosso neurônio e os valores reais de z, daí a palavra *erro* em seu nome.

$≤ft(zp-z\right)$

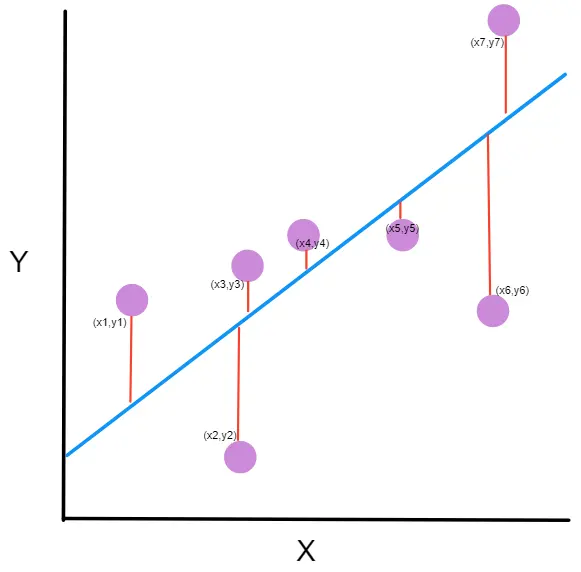
No entanto, às vezes essa distância será positiva e às vezes negativa, dependendo se se toma primeiro o valor previsto pelo nosso neurônio ou o valor de z, por isso essa distância é elevada ao quadrado, daí a palavra *quadrático* no nome.

$≤ft(zp-z\right)2$

Por fim, somam-se todas as distâncias elevadas ao quadrado e divide-se pelo número de amostras, ou seja, faz-se uma média de todo dia, daí a palavra *média* no nome.

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Já temos a maneira de calcular o ECM (erro quadrático médio).

No nosso caso, nossa perda é

	
		def loss(z, z_p):
    n = len(z)
    loss = np.sum((z_p-z) ** 2) / n
    return loss
	
	
		
	
	Copied

	
		error = loss(z, z_p)
error
	
	
		
	
	Copied

	
		103.72263739946467

Embora isso não nos diga muito, é preciso lembrar que estamos buscando o mínimo da função de erro, portanto devemos procurar um valor próximo de 0.

Vejamos como a função de perda (loss) muda em função do valor de ```a

```

	
		posibles_a = np.linspace(0, 4, 30)
perdidas = np.empty_like(posibles_a)
 
for i in range (30):
    z_p = posibles_a[i]*x
    perdidas[i] = loss(z, z_p)
 
plt.plot(posibles_a, perdidas)
plt.xlabel('a')
plt.ylabel('loss  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Podemos ver que o erro ou perda é menor quando a vale em torno de 2. Você poderia pensar, pronto, problema resolvido, e é verdade. Mas, como te disse, íamos começar com o problema mais simples, então olhando um gráfico podemos resolver.

Se o problema tivesse 2 parâmetros, poderíamos analisar um gráfico de 3 dimensões para buscar o mínimo.

Mas assim que o nosso problema tivesse mais de 2 parâmetros já não poderíamos buscar o erro mínimo com um gráfico. Sem falar que as redes neurais têm milhões de parâmetros, por exemplo, a rede neural resnet18 (que estudaremos mais adiante) é uma rede pequena e tem cerca de 11 milhões de parâmetros. É impossível buscar o erro mínimo aí de maneira manual. Portanto, precisamos de um método automático por meio de cálculos.

Descida do gradiente

Como dissemos, precisamos encontrar o valor de a que faça com que a função de perda seja mínima e, ao mesmo tempo, fazê-lo por meio de um algoritmo.

Uma das peculiaridades de um mínimo de uma função é que seu gradiente ou derivada é 0.

Se você não sabe o que é a derivada ou gradiente, a derivada de uma função em um ponto representa a inclinação da reta tangente à função nesse ponto.

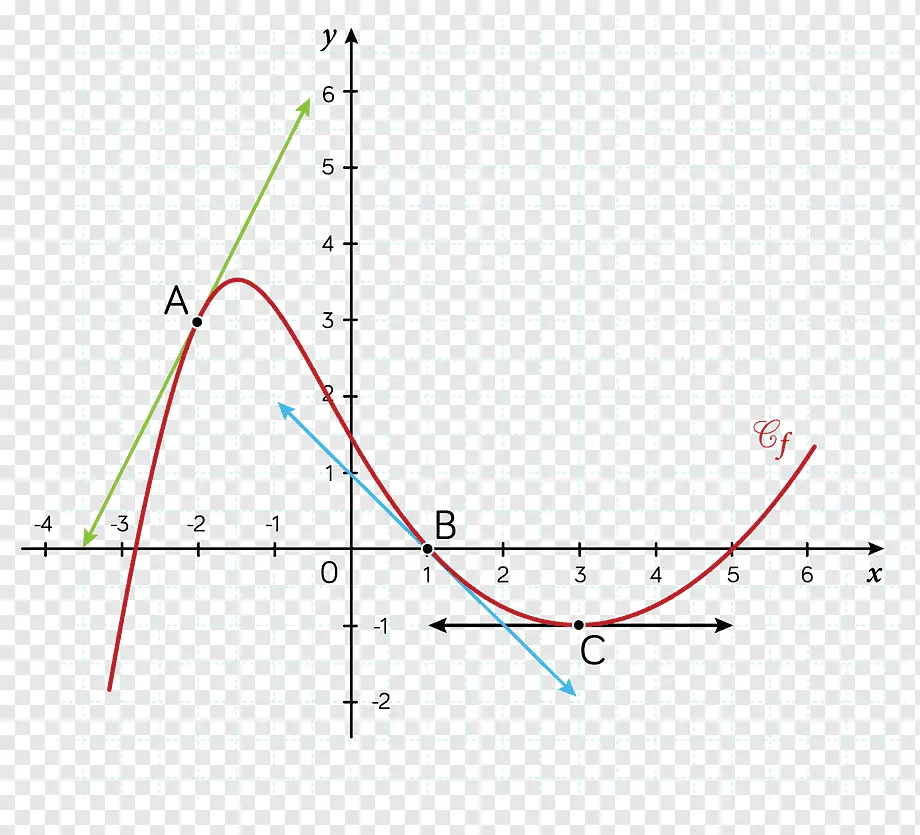
Por exemplo, nesta imagem, a derivada de A, B e C são as linhas verde, azul e preta, respectivamente

A derivada mede a inclinação de uma função; quanto mais inclinada a função em um ponto, mais perpendicular ao *eixo x* será a derivada nesse ponto, e quanto menos inclinada a função em um ponto, mais paralela ao *eixo x* será a derivada nesse ponto.

Como se calcula o gradiente da função de perda em relação a a? A função de perda tínhamos dito que era.

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Pois bem, se a derivarmos em relação a a temos

$\partial loss\partial a = \partial ≤ft(∑i=1N ≤ft(zp-z\right)2N\right)\partial a = \partial ≤ft(∑i=1N ≤ft(ax-z\right)2N\right)\partial a = 2N∑i=1N {≤ft(ax-z\right) x} = 2N∑i=1N {≤ft(zp-z\right) x}$

Se voltarmos a ver o gráfico da função de perda em relação ao valor de a, quanto maior for a inclinação da função, ou seja, quanto maior for a derivada, mais longe estaremos do mínimo. E quanto menor for a derivada, menor inclinação, mais perto estaremos do mínimo.

	
		def gradiente (a, x, z):
    # Función que calcula el valor de una derivada en un punto
    n = len(z)
    return 2*np.sum((a*x - z)*x)/n
	
	
		
	
	Copied

	
		def gradiente_linea (i, a=None, error=None, gradiente=None):
    # Función que devuleve los puntos de la linea que supone la derivada de una 
    # función en un punto dado
    if a is None:
        x1 = posibles_a[i]-0.7
        x2 = posibles_a[i]
        x3 = posibles_a[i]+0.7
 
        b = perdidas[i] - gradientes[i]*posibles_a[i]
 
        z1 = gradientes[i]*x1 + b
        z2 = perdidas[i]
        z3 = gradientes[i]*x3 + b
    else:
        x1 = a-0.7
        x2 = a
        x3 = a+0.7
 
        b = error - gradiente*a
 
        z1 = gradiente*x1 + b
        z2 = error
        z3 = gradiente*x3 + b
 
    x_linea = np.array([x1, x2, x3])
    z_linea = np.array([z1, z2, z3])
 
    return x_linea, z_linea
	
	
		
	
	Copied

	
		posibles_a = np.linspace(0, 4, 30)
perdidas = np.empty_like(posibles_a)
gradientes = np.empty_like(posibles_a)
 
for i in range (30):
    z_p = posibles_a[i]*x
    perdidas[i] = loss(z, z_p)
    gradientes[i] = gradiente(posibles_a[i], x, z) # Estos son los valores de las derivadas en cada valor de a
                                                    # es decir, nos da el valor de la pendiente de la recta tangente
                                                    # a la curva
 
# Se calcula la linea del gradiente en el inicio
i_inicio = 3
x_inicio, z_inicio = gradiente_linea(i_inicio)
 
# Se calcula la linea del gradiente en la base
i_base = 14
x_base, z_base = gradiente_linea (i_base)
 
# Se calcula la linea del gradiente al final
i_final = -3
x_final, z_final = gradiente_linea (i_final)
 
# Se dibuja el error en función de a
plt.plot(posibles_a, perdidas, linewidth = 3)
# Se dibuja la derivada al inicio
plt.plot(x_inicio, z_inicio, 'g')
plt.scatter(posibles_a[i_inicio], perdidas[i_inicio], c='green')
# Se dibuja la derivada en el medio
plt.plot(x_base, z_base, 'y')
plt.scatter(posibles_a[i_base], perdidas[i_base], c='pink')
# Se dibuja la derivada al final
plt.plot(x_final, z_final, 'r')
plt.scatter(posibles_a[i_final], perdidas[i_final], c='red')
 
plt.xlabel('a')
plt.ylabel('loss     ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como pode-se ver, no início do gráfico, estamos longe do mínimo, por isso a derivada da função (linha verde) é muito íngreme, assim como no final da função (linha vermelha). No entanto, quando estamos perto do mínimo a derivada é pequena (linha amarela).

Lembre-se, o que queremos é modificar o valor de a para que a função de custo seja mínima. Isso significa que o erro em todos os pares (x, z) será o menor possível. Pois bem, já temos uma maneira de saber o quão longe ou perto estamos desse mínimo. Agora precisamos saber como modificar a para que esteja na região de mínimo custo.

A forma de fazer isso é através do **descenso do gradiente** ou **gradient descent** em inglês. O que vamos fazer é modificar o valor de a em função do valor do gradiente.

$a' = a - α\partial loss\partial a$

Como pode-se ver, de a subtrai-se a derivada da função de perda multiplicada por $α$ , que é conhecida como **taxa de aprendizado** ou **learning rate** em inglês. Vamos ver isso por partes.

Primeiro, de a se subtrai a derivada da função de perda, vejamos por quê. Suponhamos que estamos no primeiro ponto da função de custo (o da linha verde), como vimos sua derivada tem uma grande inclinação, mas além disso ela é negativa (pois se nos deslocamos da esquerda para a direita a derivada vai para baixo), então se de a subtraímos um valor negativo, na verdade o que estamos fazendo é somar um valor a ele, ou seja, estamos fazendo com que a seja maior, aproximando-o assim da zona do mínimo.

Agora ao contrário, suponha que estamos no último ponto (o da linha vermelha), nesse ponto a derivada tem uma grande inclinação, mas além disso é positiva (já que se nos deslocamos da esquerda para a direita a derivada vai para cima). Nesse ponto, portanto, estamos subtraindo de a um número positivo, ou seja, estamos tornando a menor, estamos aproximando-a da região do mínimo.

Vamos ver agora o que significa o **learning rate** $α$ .

Este é um fator de aprendizado que nós escolhemos, ou seja, estamos configurando com que velocidade a irá se mover. Ou seja, estamos configurando a taxa de aprendizado da rede neural. Quanto maior for $α$ , mais rápido a rede irá aprender, enquanto quanto menor, mais lentamente ela irá aprender.

Mais adiante, estudaremos o que acontece ao mudar o valor de $α$ , mas por enquanto lembre-se de que valores típicos de $α$ estão entre $10 -3$ e $10 -4$ .

Loop de treinamento

Já temos uma maneira de saber o erro que o valor escolhido de a nos introduz e uma fórmula para modificar o valor de a. Agora só falta repetir este loop várias vezes até chegarmos ao mínimo da função de custo.

	
		lr = 10**-3 # Tasa de aprendizaje o learning rate
steps = 100 # Numero de veces que se realiza el bucle de enrtenamiento
 
# Matrices donde se guardarán los datos para luego ver la evolución del entrenamiento en una gráfica
Zs = np.empty([steps, len(x)])
Xs_linea_gradiente = np.empty([steps, len(x_inicio)])
Zs_linea_gradiente = np.empty([steps, len(z_inicio)])
As = np.empty(steps)
Errores = np.empty(steps)
 
for i in range(steps):
    # Calculamos el gradiente
    dl = gradiente(a, x, z)
 
    # Corregimos el valor de a
    a = a - lr*dl
 
    # Calculamos los valores que obtiene la red neuronal
    z_p = a*x
 
    # Obtenemos el error
    error = loss(z_p, z)
 
    # Obtenemos las rectas de los gradientes para representarlas
    x_linea_gradiente, z_linea_gradiente = gradiente_linea(i_inicio, a=a, error=error, gradiente=dl)
 
    # Guardamos los valores para luego ver la evolución del entrenamiento en una gráfica
    As[i] = a
    Zs[i,:] = z_p
    Errores[i] = error
    Xs_linea_gradiente[i,:] = x_linea_gradiente
    Zs_linea_gradiente[i,:] = z_linea_gradiente
 
    # Imprimimos la evolución del entrenamiento
    if (i+1)%10 == 0:
        print(f"i={i+1}: error={error}, gradiente={dl}, a={a}")
	
	
		
	
	Copied

	
		i=10: error=28.075728775043547, gradiente=-61.98100236918255, a=1.1394358551489718
i=20: error=9.50524503591466, gradiente=-30.709631939506394, a=1.569284692740735
i=30: error=4.946395605365449, gradiente=-15.215654116766258, a=1.7822612353503635
i=40: error=3.8272482302958437, gradiente=-7.5388767490642445, a=1.887784395436304
i=50: error=3.552509863476323, gradiente=-3.7352756707945205, a=1.9400677933076504
i=60: error=3.4850646173147437, gradiente=-1.8507112931062708, a=1.9659725680580205
i=70: error=3.4685075514689503, gradiente=-0.9169690786711168, a=1.978807566971417
i=80: error=3.464442973977972, gradiente=-0.4543292594425819, a=1.9851669041474533
i=90: error=3.4634451649256888, gradiente=-0.22510581958202128, a=1.9883177551597053
i=100: error=3.463200213782052, gradiente=-0.111532834297016, a=1.989878902465877

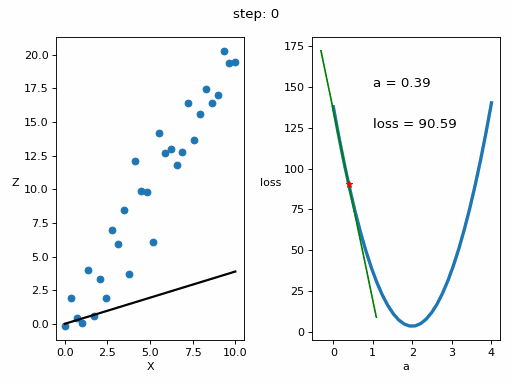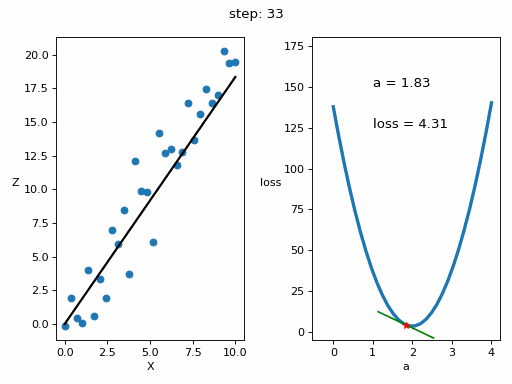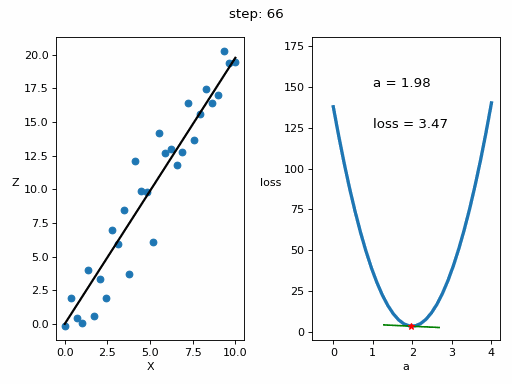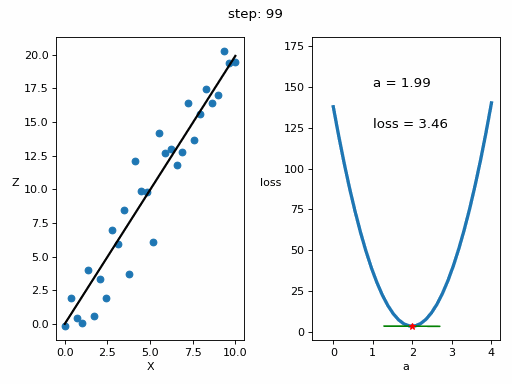
Vamos representar em um gráfico a evolução do treinamento

	
		# Creamos GIF con la evolución del entrenamiento
 
from matplotlib.animation import FuncAnimation
from IPython.display import display, Image
 
# Creamos la gráfica inicial
fig, (ax1, ax2) = plt.subplots(1,2)
fig.set_tight_layout(True)
ax1.set_xlabel('X')
ax1.set_ylabel('Z  ', rotation=0)
ax2.set_xlabel('a')
ax2.set_ylabel('loss     ', rotation=0)
 
# Se dibujan los datos que persistiran en toda la evolución de la gráfica
ax1.scatter(x, z)
ax2.plot(posibles_a, perdidas, linewidth = 3)
 
# Se dibuja el resto de lineas que irán cambiando durante el entrenamiento
line1, = ax1.plot(x, Zs[0,:], 'k', linewidth=2) # Recta generada con la pendiente a aprendida
line2, = ax2.plot(Xs_linea_gradiente[0,:], Zs_linea_gradiente[0,:], 'g') # Gradiente de la función de error
punto2, = ax2.plot(As[0], Errores[0], 'r*') # Punto donde se calcula el gradiente
 
# Se dibujan textos dentro de la segunda figura del subplot
fontsize = 12
a_text = ax2.text(1, 150, f'a = {As[0]:.2f}', fontsize = fontsize)
error_text = ax2.text(1, 125, f'loss = {Errores[0]:.2f}', fontsize = fontsize)
 
# Se dibuja un título
titulo = fig.suptitle(f'step: {0}', fontsize=fontsize)
 
# Se define la función que va a modificar la gráfica con la evolución del entrenamiento
def update(i):
    # Se actualiza la linea 1. Recta generada con la pendiente a aprendida
    line1.set_ydata(Zs[i,:])
    
    # Se actualiza la linea 2. Gradiente de la función de error
    line2.set_xdata(Xs_linea_gradiente[i,:])
    line2.set_ydata(Zs_linea_gradiente[i,:])
 
    # Se actualiza el punto 2. Punto donde se calcula el gradiente
    punto2.set_xdata([As[i]])
    punto2.set_ydata([Errores[i]])
 
    # Se actualizan los textos
    a_text.set_text(f'a = {As[i]:.2f}')
    error_text.set_text(f'loss = {Errores[i]:.2f}')
    titulo.set_text(f'step: {i}')
 
    return line1, ax1, line2, punto2, ax2, a_text, error_text
 
# Se crea la animación con un refresco cada 200 ms
interval = 200 # ms
anim = FuncAnimation(fig, update, frames=np.arange(0, steps), interval=interval)
 
# Se guarda la animación en un gif
gif_name = "GIFs/entrenamiento_regresion.gif"
anim.save(gif_name, dpi=80, writer='pillow')
 
# Leer el GIF y mostrarlo
with open(gif_name, 'rb') as f:
    display(Image(data=f.read()))
 
# Se elimina la figura para que no se muestre en el notebook
plt.close()
	
	
		
	
	Copied

	
		&lt;IPython.core.display.Image object&gt;

Vamos explicar o processo novamente, mas sem nos deter tanto em cada detalhe para reforçar os conceitos.

Temos os seguintes valores x e y

	
		x = np.array( [ 0. , 0.34482759, 0.68965517, 1.03448276, 1.37931034,
        1.72413793, 2.06896552, 2.4137931 , 2.75862069, 3.10344828,
        3.44827586, 3.79310345, 4.13793103, 4.48275862, 4.82758621,
        5.17241379, 5.51724138, 5.86206897, 6.20689655, 6.55172414,
        6.89655172, 7.24137931, 7.5862069 , 7.93103448, 8.27586207,
        8.62068966, 8.96551724, 9.31034483, 9.65517241, 10. ])
 
z = np.array( [-0.16281253, 1.88707606, 0.39649312, 0.03857752, 4.0148778 ,
        0.58866234, 3.35711859, 1.94314906, 6.96106424, 5.89792585,
        8.47226615, 3.67698542, 12.05958678, 9.85234481, 9.82181679,
        6.07652248, 14.17536744, 12.67825433, 12.97499286, 11.76098542,
       12.7843083 , 16.42241036, 13.67913705, 15.55066478, 17.45979602,
       16.41982806, 17.01977617, 20.28151197, 19.38148414, 19.41029831])
 
plt.scatter(x, z)
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Assim, usamos um único neurônio para tentar encontrar a reta que melhor se adapta a esses pontos.

Só precisamos encontrar o melhor valor possível de a

Começamos inicializando a com um valor aleatório

	
		random.seed(45)
a = random.random()
a
	
	
		
	
	Copied

	
		0.2718754143840908

Calculamos os valores z que a neurônio gera com o valor de a que acabamos de inicializar.

	
		z_p = a*x
 
plt.scatter(x, z)
plt.plot(x, z_p, 'k')
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Mas vemos que, com o valor de a que estabelecemos, o neurônio não é capaz de se assemelhar aos pontos.

Precisamos saber quão bom ou ruim é o valor de a, de modo que calculamos o erro da saída do neurônio em relação aos dados que temos. Para isso usamos o erro quadrático médio (EQM) ou mean squared error (MSE) através da fórmula

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Neste momento, nosso erro é

	
		error = loss(z, z_p)
error
	
	
		
	
	Copied

	
		103.72263739946467

Como já temos uma maneira de medir o erro, queremos diminuir o erro, de modo que buscamos que o gradiente do erro em relação a a seja zero, ou o mais próximo possível de zero. Para isso, fazemos um loop de treinamento no qual modificamos o valor de a através da fórmula

$a' = a - α\partial loss\partial a$

Onde $α$ é denominado taxa de aprendizado ou learning rate e determina a velocidade de aprendizado.

	
		lr = 10**-3 # Tasa de aprendizaje o learning rate
steps = 100 # Numero de veces que se realiza el bucle de enrtenamiento
 
# Matrices donde se guardarán los datos para luego ver la evolución del entrenamiento en una gráfica
Zs = np.empty([steps, len(x)])
Xs_linea_gradiente = np.empty([steps, len(x_inicio)])
Zs_linea_gradiente = np.empty([steps, len(z_inicio)])
As = np.empty(steps)
Errores = np.empty(steps)
 
for i in range(steps):
    # Calculamos el gradiente
    dl = gradiente(a, x, z)
 
    # Corregimos el valor de a
    a = a - lr*dl
 
    # Calculamos los valores que obtiene la red neuronal
    z_p = a*x
 
    # Obtenemos el error
    error = loss(z, z_p)
 
    # Obtenemos las rectas de los gradientes para representarlas
    x_linea_gradiente, z_linea_gradiente = gradiente_linea(i_inicio, a=a, error=error, gradiente=dl)
 
    # Guardamos los valores para luego ver la evolución del entrenamiento en una gráfica
    As[i] = a
    Zs[i,:] = z_p
    Errores[i] = error
    Xs_linea_gradiente[i,:] = x_linea_gradiente
    Zs_linea_gradiente[i,:] = z_linea_gradiente
 
    # Imprimimos la evolución del entrenamiento
    if (i+1)%10 == 0:
        print(f"i={i+1}: error={error}, gradiente={dl}, a={a}")
	
	
		
	
	Copied

	
		i=10: error=28.075728775043547, gradiente=-61.98100236918255, a=1.1394358551489718
i=20: error=9.50524503591466, gradiente=-30.709631939506394, a=1.569284692740735
i=30: error=4.946395605365449, gradiente=-15.215654116766258, a=1.7822612353503635
i=40: error=3.8272482302958437, gradiente=-7.5388767490642445, a=1.887784395436304
i=50: error=3.552509863476323, gradiente=-3.7352756707945205, a=1.9400677933076504
i=60: error=3.4850646173147437, gradiente=-1.8507112931062708, a=1.9659725680580205
i=70: error=3.4685075514689503, gradiente=-0.9169690786711168, a=1.978807566971417
i=80: error=3.464442973977972, gradiente=-0.4543292594425819, a=1.9851669041474533
i=90: error=3.4634451649256888, gradiente=-0.22510581958202128, a=1.9883177551597053
i=100: error=3.463200213782052, gradiente=-0.111532834297016, a=1.989878902465877

Vemos que o erro diminuiu consideravelmente, de 103,72 que tínhamos inicialmente para 3,46 que temos agora.

Representamos a evolução do treinamento para vê-la graficamente

Continuar lendo

Redes Neurais: História, Inverno da IA, o Breakthrough de 2012 e o mainstream de 2022

Aprenda como funcionam as redes neurais, sua história desde os anos 50, o Inverno da IA e como o ImageNet revolucionou a IA em 2012. Guia para iniciantes.

Elicitação MCP: Implementar Elicitação em Servidores com FastMCP e Python

Aprenda a implementar elicitação em servidores MCP (Model Context Protocol) com FastMCP. Tutorial completo passo a passo para criar um agente inteligente de reservas de viagens que solicita informações do usuário de forma interativa. Inclui código de servidor e cliente, configuração de ambientes virtuais com uv, e exemplos práticos de elicitação para coleta de dados do usuário em tempo real.

MCP Durabilidade: Servidor e Cliente com Persistência para Tarefas de Longa Duração

Aprenda a construir servidor e cliente MCP com durabilidade para tarefas de longa duração. Tutorial completo do Model Context Protocol com persistência de dados usando SQLite, gerenciamento de tarefas em background e monitoramento em tempo real. Implemente migração de dados, processamento em lote e treinamento de modelos ML que sobrevivem a reinicializações do servidor. Código Python com FastMCP, recursos, ferramentas e padrões de durabilidade para aplicações enterprise.

Últimos posts -->

Você viu esses projetos?

Horeca chatbot

Naviground

Subtify

Ver todos os projetos -->

Quer aplicar IA no seu projeto? Entre em contato!

Quer melhorar com essas dicas?

o1 prompt engineering

Criar prompts melhores para o1 seguindo um exemplo

Memory profiler

Ver o uso de memória de um script

DataLoader com pin_memory e num_workers

Aumentar o desempenho de DataLoader com pin_memory e num_workers

Últimos tips -->

Use isso localmente

Os espaços do Hugging Face nos permitem executar modelos com demos muito simples, mas e se a demo quebrar? Ou se o usuário a deletar? Por isso, criei contêineres docker com alguns espaços interessantes, para poder usá-los localmente, aconteça o que acontecer. Na verdade, se você clicar em qualquer botão de visualização de projeto, ele pode levá-lo a um espaço que não funciona.