Disclaimer: This post has been translated to English using a machine translation model. Please, let me know if you find any mistakes.
Language models are getting larger, which makes them increasingly expensive and costly to run.

For example, the Llama 3 400B model, if its parameters are stored in FP32 format, each parameter therefore occupies 4 bytes, which means that just to store the model requires 400*(10e9)*4 bytes = 1.6 TB of VRAM. This amounts to 20 GPUs with 80GB of VRAM each, which are not cheap either.
But if we set aside giant models and move to more common sizes, for example, 70B parameters, just storing the model requires 70*(10e9)*4 bytes = 280 GB of VRAM, which means 4 GPUs with 80GB of VRAM each.
This is because we store the weights in FP32 format, meaning that each parameter occupies 4 bytes. But what if we manage to make each parameter occupy fewer bytes? This is called quantization.
For example, if we manage to make a 70B parameter model's parameters take up half a byte, then we would only need 70*(10e9)*0.5 bytes = 35 GB of VRAM memory, which means 2 GPUs with 24GB of VRAM each, which can already be considered normal user GPUs.
We therefore need ways to reduce the size of these models. There are three ways to do this: distillation, pruning, and quantization.
Distillation involves training a smaller model based on the outputs of the larger one. That is, an input is fed to both the small and large models, and it is considered that the correct output is that of the large model, so the small model is trained according to the output of the large model. However, this requires storing the large model, which is not what we want or can do.
Pruning consists of eliminating parameters from the model, making it progressively smaller. This method is based on the idea that current language models are oversized and only a few parameters are the ones that truly provide information. Therefore, if we can eliminate the parameters that do not contribute information, we will achieve a smaller model. However, this is not straightforward today, as we do not have a good way of knowing which parameters are important and which are not.
On the other hand, quantization consists of reducing the size of each of the model's parameters. And this is what we are going to explain in this post.
Format of the parameters
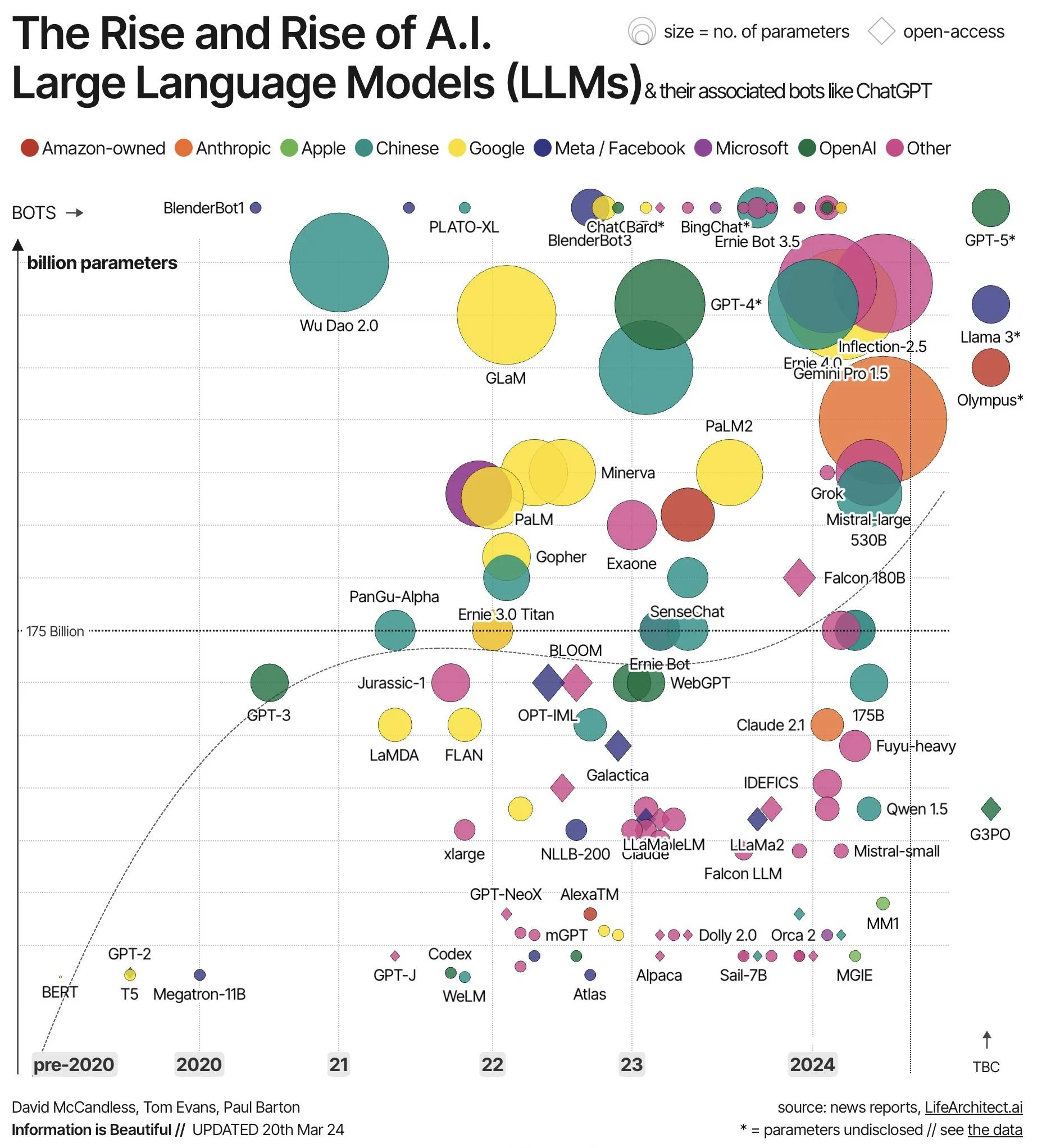
The parameters of the weights can be stored in various types of formats

Originally, FP32 was used to store the parameters, but due to running out of memory to store the models, they started switching to FP16, which did not yield bad results.
However, the problem with FP16 is that it does not reach values as high as FP32, which can lead to overflow issues. This means that during internal calculations in the network, the result may be so high that it cannot be represented in FP16, leading to errors. This happens because the model was trained in FP32, allowing all possible internal calculations to be feasible. However, when switching to FP16 for inference, some internal calculations can produce overflows.
Due to these overflow errors, TF32 and BF16 were created, which have the same number of exponent bits, allowing them to reach as high values as FP32, but with the advantage of using less memory due to having fewer bits. However, both, with fewer mantissa bits, cannot represent numbers with as much precision as FP32, which can lead to rounding errors, but at least we won't get an error when running the network. TF32 has a total of 19 bits, while BF16 has 16 bits. BF16 is more commonly used because it saves more memory.
Historically, the INT8 and UINT8 formats have existed, which can represent numbers from -128 to 127 and from 0 to 255 respectively. Although these are good formats because they allow saving memory, as each parameter occupies 1 byte compared to the 4 bytes of FP32, the problem they have is that they can only represent a small range of numbers and also only integers, which can lead to the two problems seen earlier: overflow and lack of precision.
To solve the problem that the INT8 and UINT8 formats only represent integers, the FP8 and FP4 formats have been created, but they are not yet well established, nor do they have a very standardized format.
Although we have ways to store model parameters in smaller formats, and even if we manage to solve overflow and rounding issues, we have another problem: not all GPUs are capable of representing all formats. This is because these memory issues are relatively new, so older GPUs were not designed to address these problems and therefore cannot represent all formats.
As a final detail, as a curiosity, during the training of the models, what is called mixed precision is used. The model weights are stored in FP32 format, however, the forward pass and the backward pass are performed in FP16 to make it faster. The resulting gradients from the backward pass are stored in FP16 and are used to modify the FP32 values of the weights.
Types of Quantization
Zero-Point Quantization
This is the simplest type of quantization. It consists of linearly reducing the range of values, the minimum value of FP32 corresponds to the minimum value of the new format, the zero of FP32 corresponds to the zero of the new format, and the maximum value of FP32 corresponds to the maximum value of the new format.
For example, if we want to represent numbers from -1 to 1 in UINT8 format, since the limits of UINT8 are -127 and 127, if we want to represent the value 0.3, we multiply 0.3 by 127, which gives 38.1, and round it to 38, which is the value that would be stored in UINT8.
If we want to do the opposite step, to convert 38 to a format between -1 and 1, what we do is divide 38 by 127, which gives 0.2992, which is approximately 0.3, and we can see that we have an error of 0.008
Affine Quantization
In this type of quantization, if you have an array of values in one format and you want to convert it to another, first the entire array is divided by the maximum value of the array, and then the entire array is multiplied by the maximum value of the new format.
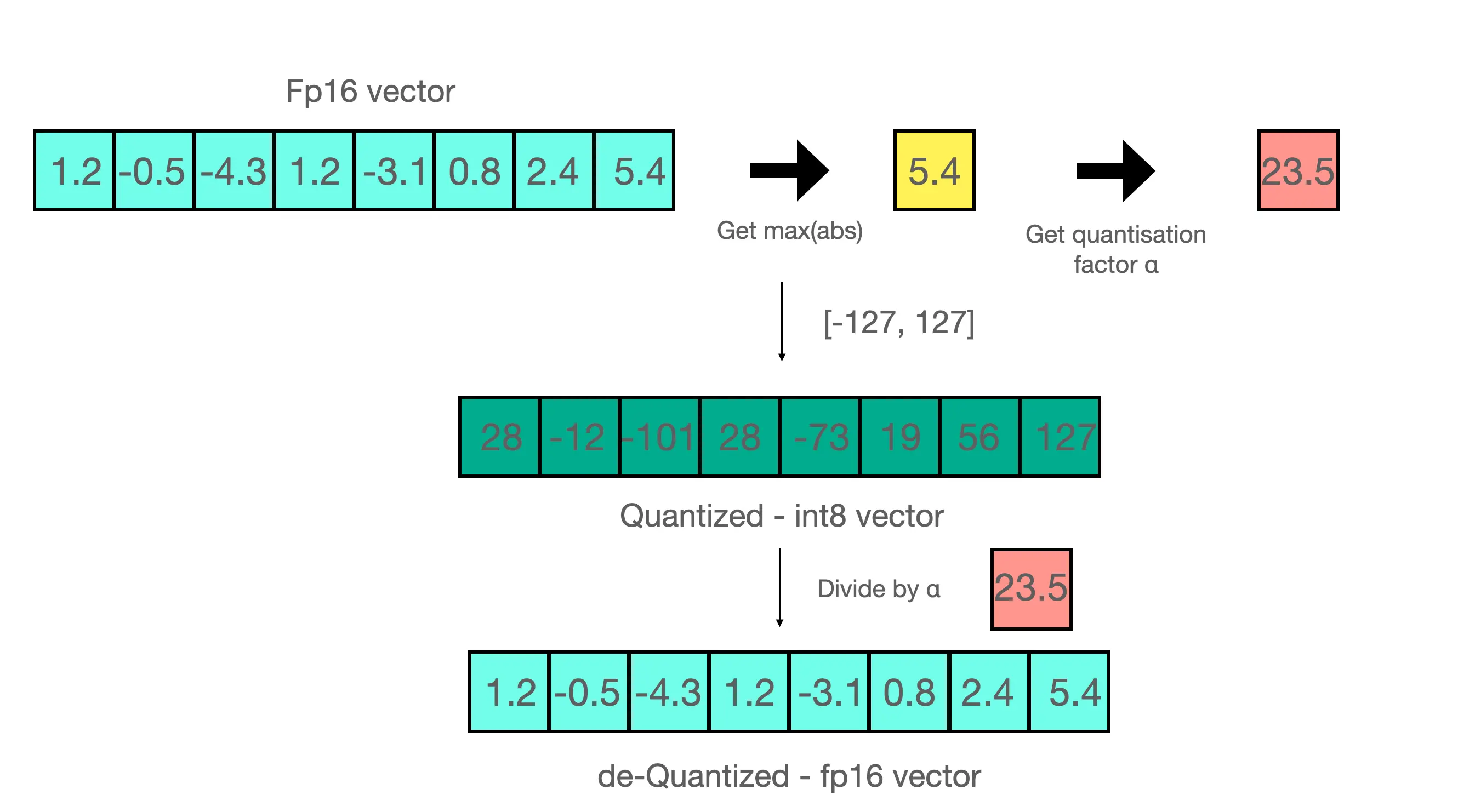
For example, in the previous image we have the array
[1.2, -0.5, -4.3, 1.2, -3.1, 0.8, 2.4, 5.4]As its maximum value is 5.4, we divide the array by that value and obtain
[0.2222222222, -0.09259259259, -0.7962962963, 0.2222222222, -0.5740740741, 0.1481481481, 0.4444444444, 1]If we now multiply all the values by 127, which is the maximum value of UINT8, we get
[28,22222222, -11.75925926, -101.1296296, 28.22222222, -72.90740741, 18.81481481, 56.44444444, 127]Which, rounding, would be
[28, -12, -101, 28, -73, 19, 56, 127]If we now wanted to perform the inverse step, we would have to divide the resulting array by 127, which would give
[0, 0.2204724409, -0.09448818898, -0.7952755906, 0.2204724409, -0.5748031496, 0.1496062992, 0.4409448819, 1]And multiply by 5.4 again, which would give us
[1, 1.190551181, -0.5102362205, -4.294488189, 1.190551181, -3.103937008, 0.8078740157, 2.381102362, 5.4]If we compare it with the original array, we see that we have an error
Moments of Quantization
Post-training Quantization
As the name suggests, quantization occurs after training. The model is trained in FP32 and then quantized to another format. This method is the simplest, but it can lead to precision errors in quantization.
Quantization during training
During training, the forward pass is performed on both the original model and a quantized model to observe potential errors arising from quantization and mitigate them. This process makes training more expensive because you need to store both the original and quantized models in memory, and slower because you have to perform the forward pass on two models.
Quantization Methods
Below I show the links to the posts where I explain each of the methods so that this post doesn't become too long
- LLM.int8()
- GPTQ
- QLoRA
- AWQ
- QuIP
- GGUF
- HQQ
- AQLM
- FBGEMM FP8