Cómo funcionan las Redes Neuronales: Regresión Lineal y Descenso del Gradiente paso a paso

04 de octubre del 2025

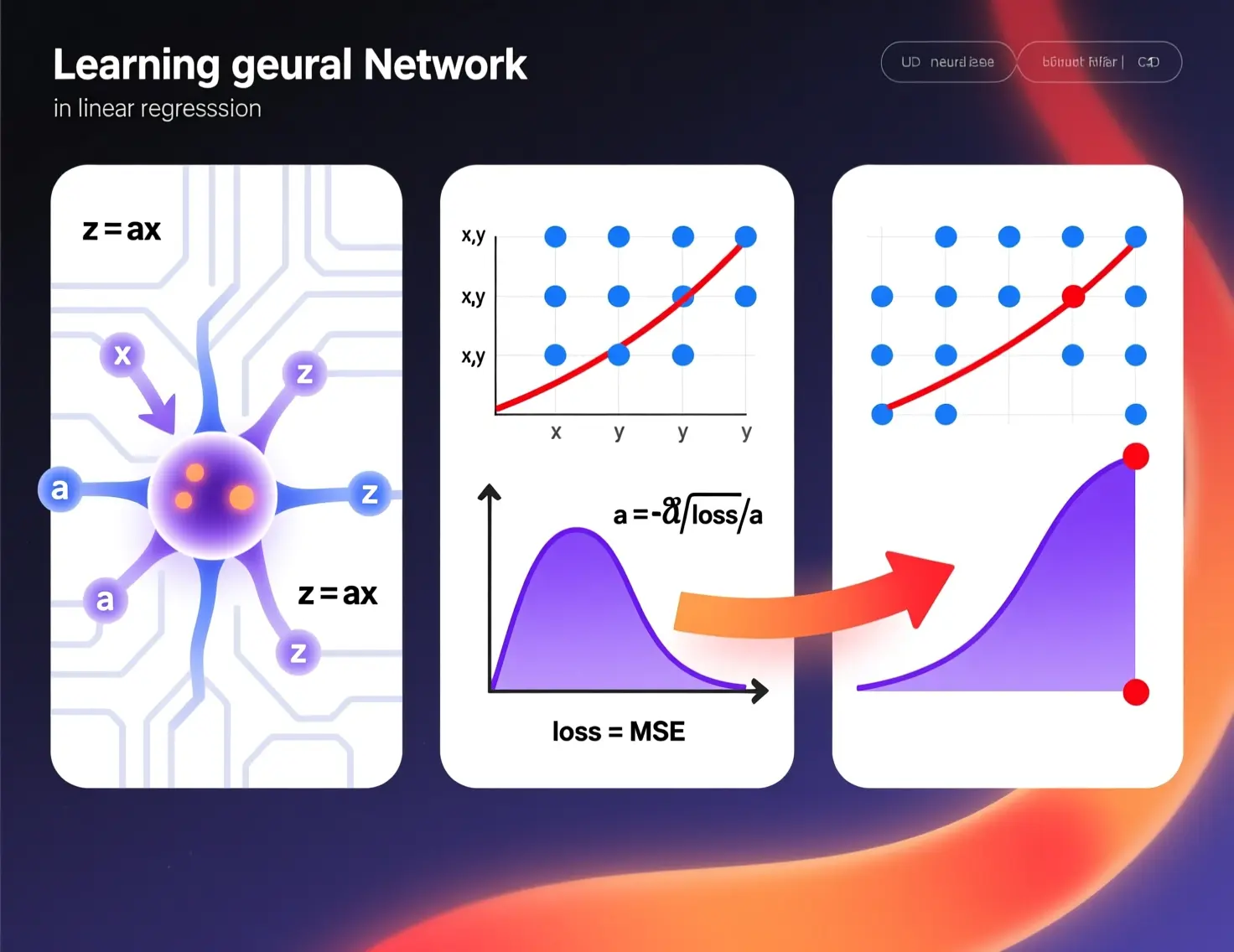
Como hemos dicho, una neurona es una unidad de procesamiento, recibe unas señales, realiza unos cálculos y saca otra señal.

!red neuronal artificial

Así que vamos a ver el ejemplo más sencillo, el caso en el que se recibe una señal y se saca otra, y lo vamos a ver con la regresión lineal.

!red neuronal regresión

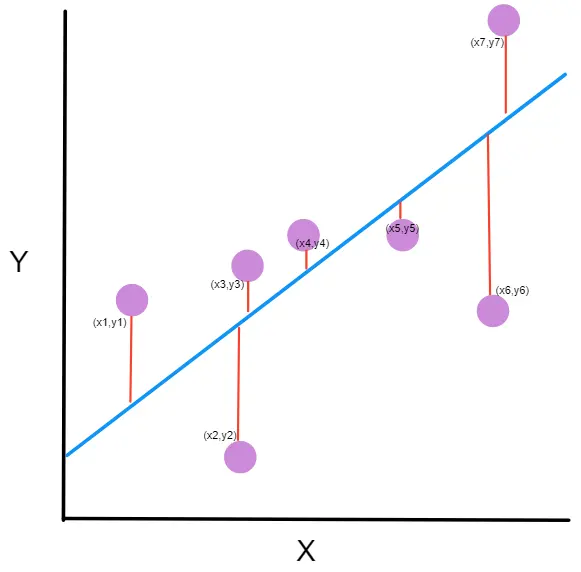
Supongamos que hemos hecho unas mediciones y obtenemos los siguientes puntos

	
		import numpy as np
 
x = np.array( [ 0. , 0.34482759, 0.68965517, 1.03448276, 1.37931034,
        1.72413793, 2.06896552, 2.4137931 , 2.75862069, 3.10344828,
        3.44827586, 3.79310345, 4.13793103, 4.48275862, 4.82758621,
        5.17241379, 5.51724138, 5.86206897, 6.20689655, 6.55172414,
        6.89655172, 7.24137931, 7.5862069 , 7.93103448, 8.27586207,
        8.62068966, 8.96551724, 9.31034483, 9.65517241, 10. ])
 
z = np.array( [-0.16281253, 1.88707606, 0.39649312, 0.03857752, 4.0148778 ,
        0.58866234, 3.35711859, 1.94314906, 6.96106424, 5.89792585,
        8.47226615, 3.67698542, 12.05958678, 9.85234481, 9.82181679,
        6.07652248, 14.17536744, 12.67825433, 12.97499286, 11.76098542,
       12.7843083 , 16.42241036, 13.67913705, 15.55066478, 17.45979602,
       16.41982806, 17.01977617, 20.28151197, 19.38148414, 19.41029831])
	
	
		
	
	Copied

	
		import matplotlib.pyplot as plt
 
plt.scatter(x, z)
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como vemos esto se puede asemejar a una regresión lineal. Es decir, podemos suponer que la neurona recibe x, lo multiplica por un número y saca z

!red neuronal regresión

A partir de aquí vamos a mostrar cómo funcionan las redes neuronales, sólo que con un ejemplo sencillo de una sola neurona, luego iremos mostrando ejemplos cada vez más complejos, hasta que explicaremos el funcionamiento general de las redes neuronales. Pero si entiendes lo que va a pasar a continuación vas a entender las redes neuronales.

Nuestra neurona tiene el parámetro a, que es el que queremos cambiar para que la recta que va a generar se asemeje lo máximo posible a los puntos. El proceso de aprendizaje de nuestra neurona va a consistir en, mediante unos cuantos cálculos, determinar el mejor valor posible de a

Inicialización aleatoria del parámetro

Este ejemplo es sencillo, pero cuando tenemos redes neuronales complejas y no sabemos qué valores tienen que tener sus parámetros, lo que se hace es inicializarlos aleatoriamente

	
		import random
 
random.seed(45) # Esto es una semilla, cuando se generan números aleatorios, 
                # pero queremos que siempre se genere el mismo se suele fijar
                # un número llamado semilla. Esto hace que siempre a sea el mismo
 
a = random.random()
a
	
	
		
	
	Copied

	
		0.2718754143840908

El valor de a es 0.271875, veamos qué recta saldría si paráramos ahora

	
		z_p = a*x
 
plt.scatter(x, z)
plt.plot(x, z_p, 'k')
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como vemos, no se parece en nada, así que vamos a tener que hacer que nuestra neurona *aprenda*

Cálculo del error o loss

Para buscar el mejor valor posible de a queremos encontrar un valor que haga que los valores predichos por nuestra neurona tengan el menor error posible con los valores reales de z.

En este tipo de problemas se suele utilizar el error cuadrático medio (ECM) o mean squared error (MSE) en inglés. Hay muchas más funciones de error, pero de momento no vienen al caso, así que quédate con esta y ya aprenderemos más funciones más adelante.

En la literatura a este error se le suele llamar función de pérdida o loss function, por lo que a partir de ahora lo llamaremos así.

El error cuadrático medio (ECM) mide la distancia entre los puntos predichos por nuestra neurona y los valores reales de z, de ahí la palabra *error* dentro de su nombre.

$≤ft(zp-z\right)$

Sin embargo, a veces esa distancia va a ser positiva y a veces negativa, según si se toma primero el valor predicho por nuestra neurona o el valor de z, por lo que dicha distancia se eleva al cuadrado, de ahí la palabra *cuadrático* del nombre.

$≤ft(zp-z\right)2$

Por último, se suman todas las distancias elevadas al cuadrado y se divide entre el número de muestras, vamos, lo que es hacer una media de toda la vida, de ahí la palabra *medio* del nombre.

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Ya tenemos la manera de calcular el ECM (error cuadrático medio).

En nuestro caso, nuestra pérdida es

	
		def loss(z, z_p):
    n = len(z)
    loss = np.sum((z_p-z) ** 2) / n
    return loss
	
	
		
	
	Copied

	
		error = loss(z, z_p)
error
	
	
		
	
	Copied

	
		103.72263739946467

Aunque esto no nos dice mucho, hay que recordar que buscamos el mínimo de la función de error, por lo que deberíamos buscar un valor cercano a 0.

Veamos cómo cambia la función de pérdida (loss) en función del valor de <code>a</code>

	
		posibles_a = np.linspace(0, 4, 30)
perdidas = np.empty_like(posibles_a)
 
for i in range (30):
    z_p = posibles_a[i]*x
    perdidas[i] = loss(z, z_p)
 
plt.plot(posibles_a, perdidas)
plt.xlabel('a')
plt.ylabel('loss  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Podemos ver que el error o pérdida es menor cuando a vale en torno a 2. Podrías pensar, ya está, problema solucionado, y es cierto. Pero como te dije, íbamos a empezar con el problema más sencillo, por lo que mirando una gráfica lo podemos solucionar.

Si el problema tuviese 2 parámetros, podríamos revisar un gráfico de 3 dimensiones para buscar el mínimo

!grafico 3 dimensiones

Pero en cuanto nuestro problema tuviese más de 2 parámetros ya no podríamos buscar el mínimo error con una gráfica. Por no decir que las redes neuronales tienen millones de parámetros, por ejemplo, la red neuronal resnet18 (que más tarde la estudiaremos) es una red pequeña y tiene en torno a 11 millones de parámetros. Es imposible buscar el mínimo error ahí de manera manual. De modo que necesitamos un método automático mediante cálculos.

Descenso del gradiente

Como hemos dicho, necesitamos encontrar el valor de a que haga que la función de pérdida sea mínima y, a su vez, hacerlo mediante un algoritmo.

Una de las peculiaridades de un mínimo de una función es que su gradiente o derivada es 0.

Si no sabes lo que es la derivada o gradiente, la derivada de una función en un punto representa la pendiente de la recta tangente a la función en ese punto.

!derivada

Por ejemplo, en esta imagen, la derivada de A, B y C son las líneas verde, azul y negra respectivamente

La derivada mide la pendiente de una función; cuanto más pendiente tiene la función en un punto, más perpendicular al *eje x* será la derivada en ese punto, y cuanto menos pendiente tiene la función en un punto, más paralela al *eje x* será la derivada en ese punto.

¿Cómo se calcula el gradiente de la función de pérdida con respecto a a? La función de pérdida habíamos dicho que era.

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Pues bien, si la derivamos con respecto a a nos queda

$\partial loss\partial a = \partial ≤ft(∑i=1N ≤ft(zp-z\right)2N\right)\partial a = \partial ≤ft(∑i=1N ≤ft(ax-z\right)2N\right)\partial a = 2N∑i=1N {≤ft(ax-z\right) x} = 2N∑i=1N {≤ft(zp-z\right) x}$

Si volvemos a ver la gráfica de la función de pérdida con respecto al valor de a, cuanto mayor pendiente tenga la función, es decir, cuanto mayor sea la derivada, más lejos estaremos del mínimo. Y cuanto menor sea la derivada, menor pendiente, más cerca estaremos del mínimo.

	
		def gradiente (a, x, z):
    # Función que calcula el valor de una derivada en un punto
    n = len(z)
    return 2*np.sum((a*x - z)*x)/n
	
	
		
	
	Copied

	
		def gradiente_linea (i, a=None, error=None, gradiente=None):
    # Función que devuleve los puntos de la linea que supone la derivada de una 
    # función en un punto dado
    if a is None:
        x1 = posibles_a[i]-0.7
        x2 = posibles_a[i]
        x3 = posibles_a[i]+0.7
 
        b = perdidas[i] - gradientes[i]*posibles_a[i]
 
        z1 = gradientes[i]*x1 + b
        z2 = perdidas[i]
        z3 = gradientes[i]*x3 + b
    else:
        x1 = a-0.7
        x2 = a
        x3 = a+0.7
 
        b = error - gradiente*a
 
        z1 = gradiente*x1 + b
        z2 = error
        z3 = gradiente*x3 + b
 
    x_linea = np.array([x1, x2, x3])
    z_linea = np.array([z1, z2, z3])
 
    return x_linea, z_linea
	
	
		
	
	Copied

	
		posibles_a = np.linspace(0, 4, 30)
perdidas = np.empty_like(posibles_a)
gradientes = np.empty_like(posibles_a)
 
for i in range (30):
    z_p = posibles_a[i]*x
    perdidas[i] = loss(z, z_p)
    gradientes[i] = gradiente(posibles_a[i], x, z) # Estos son los valores de las derivadas en cada valor de a
                                                    # es decir, nos da el valor de la pendiente de la recta tangente
                                                    # a la curva
 
# Se calcula la linea del gradiente en el inicio
i_inicio = 3
x_inicio, z_inicio = gradiente_linea(i_inicio)
 
# Se calcula la linea del gradiente en la base
i_base = 14
x_base, z_base = gradiente_linea (i_base)
 
# Se calcula la linea del gradiente al final
i_final = -3
x_final, z_final = gradiente_linea (i_final)
 
# Se dibuja el error en función de a
plt.plot(posibles_a, perdidas, linewidth = 3)
# Se dibuja la derivada al inicio
plt.plot(x_inicio, z_inicio, 'g')
plt.scatter(posibles_a[i_inicio], perdidas[i_inicio], c='green')
# Se dibuja la derivada en el medio
plt.plot(x_base, z_base, 'y')
plt.scatter(posibles_a[i_base], perdidas[i_base], c='pink')
# Se dibuja la derivada al final
plt.plot(x_final, z_final, 'r')
plt.scatter(posibles_a[i_final], perdidas[i_final], c='red')
 
plt.xlabel('a')
plt.ylabel('loss     ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Como se puede ver, al inicio de la gráfica, estamos lejos del mínimo, por lo que la derivada de la función (línea verde) es muy empinada, igual que al final de la función (línea roja). Sin embargo, cuando estamos cerca del mínimo la derivada es pequeña (línea amarilla).

Recordatorio, lo que queremos es modificar el valor de a que haga que la función de costo sea mínima. Esto supone que el error en todos los pares (x, z) va a ser el menor posible. Pues bien, ya tenemos una manera de saber cuán lejos o cerca estamos de ese mínimo. Ahora necesitamos saber cómo modificar a para hacer que esté en la zona de mínimo costo.

La forma de hacer esto es mediante el **descenso del gradiente** o **gradient descent** en inglés. Lo que vamos a hacer es modificar el valor de a en función del valor del gradiente.

$a' = a - α\partial loss\partial a$

Como se puede ver, a a se le resta la derivada de la función de pérdida multiplicada por $α$ , que se conoce como **tasa de aprendizaje** o **learning rate** en inglés. Vamos a ver esto por partes.

Primero, a a se le resta la derivada de la función de pérdida, veamos por qué. Supongamos que estamos en el primer punto de la función de coste (el de la línea verde), como hemos visto su derivada tiene una gran pendiente, pero además esta es negativa (ya que si nos desplazamos de izquierda a derecha la derivada va hacia abajo), por lo que si a a se le resta un valor negativo, en realidad lo que estamos haciendo es sumarle un valor, es decir, estamos haciendo que a sea mayor, por lo que lo estamos acercando a la zona del mínimo.

Ahora al revés, supongamos que estamos en el último punto (el de la línea roja), en ese punto la derivada tiene una gran pendiente, pero además es positiva (ya que si nos desplazamos de izquierda a derecha la derivada va hacia arriba). En ese punto por tanto estamos restando a a un número positivo, es decir, estamos haciendo a a más pequeña, la estamos acercando a la zona del mínimo.

Veamos ahora qué significa el **learning rate** $α$ .

Este es un factor de aprendizaje que nosotros elegimos, es decir, estamos configurando con qué velocidad se moverá a. Es decir, estamos configurando la velocidad de aprendizaje de la red neuronal. Cuanto más grande sea $α$ , más rápido aprenderá la red, mientras que cuanto más pequeño, más lento aprenderá.

Más adelante estudiaremos qué ocurre al cambiar el valor de $α$ , pero de momento quédate con que valores típicos de $α$ son entre $10 -3$ y $10 -4$ .

Bucle de entrenamiento

Ya tenemos una manera de saber el error que nos introduce el valor de a elegido y una fórmula para modificar el valor de a. Ya solo hace falta repetir este bucle varias veces hasta que lleguemos al mínimo de la función de coste.

	
		lr = 10**-3 # Tasa de aprendizaje o learning rate
steps = 100 # Numero de veces que se realiza el bucle de enrtenamiento
 
# Matrices donde se guardarán los datos para luego ver la evolución del entrenamiento en una gráfica
Zs = np.empty([steps, len(x)])
Xs_linea_gradiente = np.empty([steps, len(x_inicio)])
Zs_linea_gradiente = np.empty([steps, len(z_inicio)])
As = np.empty(steps)
Errores = np.empty(steps)
 
for i in range(steps):
    # Calculamos el gradiente
    dl = gradiente(a, x, z)
 
    # Corregimos el valor de a
    a = a - lr*dl
 
    # Calculamos los valores que obtiene la red neuronal
    z_p = a*x
 
    # Obtenemos el error
    error = loss(z_p, z)
 
    # Obtenemos las rectas de los gradientes para representarlas
    x_linea_gradiente, z_linea_gradiente = gradiente_linea(i_inicio, a=a, error=error, gradiente=dl)
 
    # Guardamos los valores para luego ver la evolución del entrenamiento en una gráfica
    As[i] = a
    Zs[i,:] = z_p
    Errores[i] = error
    Xs_linea_gradiente[i,:] = x_linea_gradiente
    Zs_linea_gradiente[i,:] = z_linea_gradiente
 
    # Imprimimos la evolución del entrenamiento
    if (i+1)%10 == 0:
        print(f"i={i+1}: error={error}, gradiente={dl}, a={a}")
	
	
		
	
	Copied

	
		i=10: error=28.075728775043547, gradiente=-61.98100236918255, a=1.1394358551489718
i=20: error=9.50524503591466, gradiente=-30.709631939506394, a=1.569284692740735
i=30: error=4.946395605365449, gradiente=-15.215654116766258, a=1.7822612353503635
i=40: error=3.8272482302958437, gradiente=-7.5388767490642445, a=1.887784395436304
i=50: error=3.552509863476323, gradiente=-3.7352756707945205, a=1.9400677933076504
i=60: error=3.4850646173147437, gradiente=-1.8507112931062708, a=1.9659725680580205
i=70: error=3.4685075514689503, gradiente=-0.9169690786711168, a=1.978807566971417
i=80: error=3.464442973977972, gradiente=-0.4543292594425819, a=1.9851669041474533
i=90: error=3.4634451649256888, gradiente=-0.22510581958202128, a=1.9883177551597053
i=100: error=3.463200213782052, gradiente=-0.111532834297016, a=1.989878902465877

Vamos a representar en una gráfica la evolución del entrenamiento

	
		# Creamos GIF con la evolución del entrenamiento
 
from matplotlib.animation import FuncAnimation
from IPython.display import display, Image
 
# Creamos la gráfica inicial
fig, (ax1, ax2) = plt.subplots(1,2)
fig.set_tight_layout(True)
ax1.set_xlabel('X')
ax1.set_ylabel('Z  ', rotation=0)
ax2.set_xlabel('a')
ax2.set_ylabel('loss     ', rotation=0)
 
# Se dibujan los datos que persistiran en toda la evolución de la gráfica
ax1.scatter(x, z)
ax2.plot(posibles_a, perdidas, linewidth = 3)
 
# Se dibuja el resto de lineas que irán cambiando durante el entrenamiento
line1, = ax1.plot(x, Zs[0,:], 'k', linewidth=2) # Recta generada con la pendiente a aprendida
line2, = ax2.plot(Xs_linea_gradiente[0,:], Zs_linea_gradiente[0,:], 'g') # Gradiente de la función de error
punto2, = ax2.plot(As[0], Errores[0], 'r*') # Punto donde se calcula el gradiente
 
# Se dibujan textos dentro de la segunda figura del subplot
fontsize = 12
a_text = ax2.text(1, 150, f'a = {As[0]:.2f}', fontsize = fontsize)
error_text = ax2.text(1, 125, f'loss = {Errores[0]:.2f}', fontsize = fontsize)
 
# Se dibuja un título
titulo = fig.suptitle(f'step: {0}', fontsize=fontsize)
 
# Se define la función que va a modificar la gráfica con la evolución del entrenamiento
def update(i):
    # Se actualiza la linea 1. Recta generada con la pendiente a aprendida
    line1.set_ydata(Zs[i,:])
    
    # Se actualiza la linea 2. Gradiente de la función de error
    line2.set_xdata(Xs_linea_gradiente[i,:])
    line2.set_ydata(Zs_linea_gradiente[i,:])
 
    # Se actualiza el punto 2. Punto donde se calcula el gradiente
    punto2.set_xdata([As[i]])
    punto2.set_ydata([Errores[i]])
 
    # Se actualizan los textos
    a_text.set_text(f'a = {As[i]:.2f}')
    error_text.set_text(f'loss = {Errores[i]:.2f}')
    titulo.set_text(f'step: {i}')
 
    return line1, ax1, line2, punto2, ax2, a_text, error_text
 
# Se crea la animación con un refresco cada 200 ms
interval = 200 # ms
anim = FuncAnimation(fig, update, frames=np.arange(0, steps), interval=interval)
 
# Se guarda la animación en un gif
gif_name = "GIFs/entrenamiento_regresion.gif"
anim.save(gif_name, dpi=80, writer='pillow')
 
# Leer el GIF y mostrarlo
with open(gif_name, 'rb') as f:
    display(Image(data=f.read()))
 
# Se elimina la figura para que no se muestre en el notebook
plt.close()
	
	
		
	
	Copied

	
		&lt;IPython.core.display.Image object&gt;

Vamos a volver a explicar el proceso, pero sin detenernos tanto en cada detalle para afianzar los conceptos

Tenemos los siguientes valores x e y

	
		x = np.array( [ 0. , 0.34482759, 0.68965517, 1.03448276, 1.37931034,
        1.72413793, 2.06896552, 2.4137931 , 2.75862069, 3.10344828,
        3.44827586, 3.79310345, 4.13793103, 4.48275862, 4.82758621,
        5.17241379, 5.51724138, 5.86206897, 6.20689655, 6.55172414,
        6.89655172, 7.24137931, 7.5862069 , 7.93103448, 8.27586207,
        8.62068966, 8.96551724, 9.31034483, 9.65517241, 10. ])
 
z = np.array( [-0.16281253, 1.88707606, 0.39649312, 0.03857752, 4.0148778 ,
        0.58866234, 3.35711859, 1.94314906, 6.96106424, 5.89792585,
        8.47226615, 3.67698542, 12.05958678, 9.85234481, 9.82181679,
        6.07652248, 14.17536744, 12.67825433, 12.97499286, 11.76098542,
       12.7843083 , 16.42241036, 13.67913705, 15.55066478, 17.45979602,
       16.41982806, 17.01977617, 20.28151197, 19.38148414, 19.41029831])
 
plt.scatter(x, z)
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Así que usamos una sola neurona para intentar encontrar la recta que mejor se adapta a dichos puntos.

!red neuronal regresión

Solo necesitamos encontrar el mejor valor de a posible

Empezamos inicializando a con un valor aleatorio

	
		random.seed(45)
a = random.random()
a
	
	
		
	
	Copied

	
		0.2718754143840908

Calculamos los valores z que genera la neurona con el valor de a que acabamos de inicializar.

	
		z_p = a*x
 
plt.scatter(x, z)
plt.plot(x, z_p, 'k')
plt.xlabel('X')
plt.ylabel('Z  ', rotation=0)
plt.show()
	
	
		
	
	Copied

	
		&lt;Figure size 640x480 with 1 Axes&gt;

Pero vemos que con el valor de a que hemos establecido, la neurona no es capaz de asemejarse a los puntos.

Necesitamos saber cuán bueno o malo es el valor de a, de modo que calculamos el error de la salida de la neurona con respecto a los datos que tenemos. Para ello usamos el error cuadrático medio (ECM) o mean squared error (MSE) mediante la fórmula

$loss = ∑i=1N ≤ft(zp-z\right)2N$

Ahora mismo, nuestro error es

	
		error = loss(z, z_p)
error
	
	
		
	
	Copied

	
		103.72263739946467

Como ya tenemos una manera de medir el error, queremos disminuir el error, de modo que buscamos que el gradiente del error con respecto a a sea cero, o lo más cercano a cero. Para ello hacemos un bucle de entrenamiento en el que modificamos el valor de a mediante la fórmula

$a' = a - α\partial loss\partial a$

Donde $α$ se denomina tasa de aprendizaje o learning rate y determina la velocidad de aprendizaje.

	
		lr = 10**-3 # Tasa de aprendizaje o learning rate
steps = 100 # Numero de veces que se realiza el bucle de enrtenamiento
 
# Matrices donde se guardarán los datos para luego ver la evolución del entrenamiento en una gráfica
Zs = np.empty([steps, len(x)])
Xs_linea_gradiente = np.empty([steps, len(x_inicio)])
Zs_linea_gradiente = np.empty([steps, len(z_inicio)])
As = np.empty(steps)
Errores = np.empty(steps)
 
for i in range(steps):
    # Calculamos el gradiente
    dl = gradiente(a, x, z)
 
    # Corregimos el valor de a
    a = a - lr*dl
 
    # Calculamos los valores que obtiene la red neuronal
    z_p = a*x
 
    # Obtenemos el error
    error = loss(z, z_p)
 
    # Obtenemos las rectas de los gradientes para representarlas
    x_linea_gradiente, z_linea_gradiente = gradiente_linea(i_inicio, a=a, error=error, gradiente=dl)
 
    # Guardamos los valores para luego ver la evolución del entrenamiento en una gráfica
    As[i] = a
    Zs[i,:] = z_p
    Errores[i] = error
    Xs_linea_gradiente[i,:] = x_linea_gradiente
    Zs_linea_gradiente[i,:] = z_linea_gradiente
 
    # Imprimimos la evolución del entrenamiento
    if (i+1)%10 == 0:
        print(f"i={i+1}: error={error}, gradiente={dl}, a={a}")
	
	
		
	
	Copied

	
		i=10: error=28.075728775043547, gradiente=-61.98100236918255, a=1.1394358551489718
i=20: error=9.50524503591466, gradiente=-30.709631939506394, a=1.569284692740735
i=30: error=4.946395605365449, gradiente=-15.215654116766258, a=1.7822612353503635
i=40: error=3.8272482302958437, gradiente=-7.5388767490642445, a=1.887784395436304
i=50: error=3.552509863476323, gradiente=-3.7352756707945205, a=1.9400677933076504
i=60: error=3.4850646173147437, gradiente=-1.8507112931062708, a=1.9659725680580205
i=70: error=3.4685075514689503, gradiente=-0.9169690786711168, a=1.978807566971417
i=80: error=3.464442973977972, gradiente=-0.4543292594425819, a=1.9851669041474533
i=90: error=3.4634451649256888, gradiente=-0.22510581958202128, a=1.9883177551597053
i=100: error=3.463200213782052, gradiente=-0.111532834297016, a=1.989878902465877

Vemos que el error ha disminuido notablemente, de 103,72 que teníamos inicialmente a 3,46 que tenemos ahora.

Representamos la evolución del entrenamiento para verla gráficamente

!GIF

Seguir leyendo

Redes Neuronales: Historia, AI Winter, el gran salto de 2012 y el mainstream del 2022

Descubre cómo funcionan las redes neuronales, su historia desde los años 50, el AI Winter y cómo ImageNet revolucionó la IA en 2012. Guía para principiantes.

Elicitación MCP: Implementar Elicitación en Servidores con FastMCP y Python

Aprende a implementar elicitación en servidores MCP (Model Context Protocol) con FastMCP. Tutorial completo paso a paso para crear un agente inteligente de reservas de viajes que solicita información al usuario de forma interactiva. Incluye código de servidor y cliente, configuración de entornos virtuales con uv, y ejemplos prácticos de elicitación para recopilar datos del usuario en tiempo real.

MCP Durability: Servidor y Cliente con Persistencia para Tareas de Larga Duración

Aprende a crear un servidor y cliente MCP con durabilidad para tareas de larga duración. Tutorial completo sobre Model Context Protocol con persistencia de datos usando SQLite, gestión de tareas en background y monitoreo en tiempo real. Implementa migración de datos, procesamiento por lotes y entrenamiento de modelos ML que sobreviven a reinicios del servidor. Código Python con FastMCP, recursos, herramientas y patrones de durabilidad para aplicaciones enterprise.

Últimos posts -->

¿Has visto estos proyectos?

Horeca chatbot

Naviground

Subtify

Ver todos los proyectos -->

¿Quieres aplicar la IA en tu proyecto? Contactame!

¿Quieres mejorar con estos tips?

o1 prompt engineering

Crear mejores prompts para o1 siguiendo un ejemplo

Memory profiler

Ver el uso de memoria de un script

DataLoader con pin_memory y num_workers

Aumentar el rendimiento de DataLoader con pin_memory y num_workers

Últimos tips -->

Usa esto en local

Los espacios de Hugging Face nos permite ejecutar modelos con demos muy sencillas, pero ¿qué pasa si la demo se rompe? O si el usuario la elimina? Por ello he creado contenedores docker con algunos espacios interesantes, para poder usarlos de manera local, pase lo que pase. De hecho, es posible que si pinchas en alún botón de ver proyecto te lleve a un espacio que no funciona.